近日，我院邓习军博士及其合作者在微分方程领域国际知名学术期刊《 Journal of Differential Equations》发表论文“Stability of 2-soliton solutions for the modified Camassa Holm equation with cubic nonlinearity”。
该文研究了一类带立方非线性项的修正CH方程在非零常数背景下的2-孤子解的稳定性。基于变分方法，通过利用关于动量变量的守恒量，严格证明了当将2-孤子解视为修正CH方程的初值问题解时，它们在 Sobolev 空间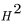 
中对于动量变量的扰动是非线性稳定的。本文为进一步研究该方程的更一般的n-孤子解的稳定性这一挑战性问题提供了重要线索。
该项成果是我院微分方程研究团队成员邓习军博士（第一作者）、美国查尔斯顿学院数学系Stéphane Lafortune教授（通讯作者）以及中国地质大学（武汉）数学学院刘志苏教授共同合作完成的。近年来邓习军博士在微分方程与动力系统这一领域取得了一系列深刻的研究成果，现已在《Journal of Differential Equations》、《Journal of Dynamics and Differential Equations》等国际权威期刊上发表多篇高水平的学术论文，目前正联合主持一项国家自然科学基金面上项目。
《Journal of Differential Equations》在JCR期刊MATHEMATICS类中排名为23/329，目前位列中国科学院分区一区TOP期刊，中国数学会认定的T2级高质量科技期刊，是微分方程与动力系统领域国际公认的最具影响力的顶尖期刊之一，对论文的原创性要求很高，拥有广泛的学术影响力和声誉。
